I know it's an old thread, but the subject has also been discussed more recently on Pouet:
http://www.pouet.net/topic.php?which=10195
The Brian version, that I've just discovered, looks so much better that I decided to give the effect a second chance; it is indeed the same effect. I haven't found any detailed analysis so I made one.
Warning: long post!
Layer 1: the two shears
-----------------------
A rotation can be decomposed into 2 shears and 2 zooms: https://en.m.wikipedia.org/wiki/Rotation_matrix#Decomposition_into_shears
Actually this is just LDU decomposition applied to a rotation matrix: in 2D, L and U are shear matrices.
The effect I am describing here performs the transformations in a different order, and furthermore doesn't do any X zoom. So a more appropriate matrix decomposition is this one:
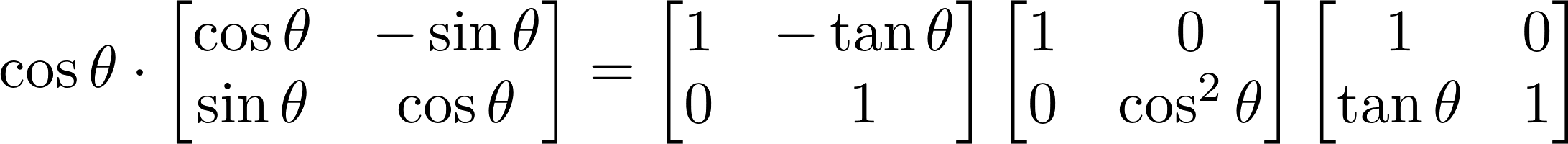
On the right-hand side, we have the transformations that the effect will perform. Reading from right to left we recognise:
- Y shear
- Y zoom
- X shear
The first one will consist of blits and is the heart of the algorithm; it is the subject of layer 3. The other two will be combined into the Copperlist.
On the left-hand side of the equation, we have what will appear on the screen: the expected rotation and, whoops, a zoom factor that we can't control. This artefact is due to the effect not performing the X zoom. Reality check: both Turmoil and Brian exhibit this artefact.
Layer 2: the quadrants
----------------------
The shears have a factor of +/- tan(theta), which can grow arbitrarily large. So the effect is typically divided into quadrants, with the canonical one between -45 and +45 degrees. Reality check: the Turmoil monster appears at a -45° angle.
All the parameters become well-behaved: the shear factors between -1 and +1, and the involontary zoom between 71% (sqrt(2) / 2) and 100%; that seems acceptable.
Presumably, pre-rotated images are used for the other quadrants. They would also need to be pre-sheared to some extent (e.g. per block of 16 pixel columns), because we only have one frame to switch between quadrants. The show must go on.
Layer 3: the Y shear
--------------------
The maths are done, but we still can't implement the effect :) The problem is that we can't actually perform an arbitrary Y shear on a large picture fast enough. The solution is to constrain the angle to a small change from the previous frame, and incrementally perform the Y shear.
More precisely, we will limit the speed of pixel columns to 1 pixel/frame. So a given column will either stay in place, or move by 1 pixel up or down. That's the key to allowing us to move multiple columns simultaneously.
Within a quadrant, the image starts sheared on one side (left will be up) and ends in the opposite shape. Right in the middle, the image will appear untransformed (0°). The centre is unaffected by the shear. So the pixels on the left half of the image will go down, while the right half will go up at the same speed.
I will call a word-aligned sequence of 16 columns a "block"; that's what we want to manipulate, for speed reasons. Within a block, a subset of the columns will move by 1 pixel, and the others won't move at all. We can do that with a single blit. Let's take the example of a downward movement. A will point to the block, one line above the first image pixel (whose position depends on the current angle). B, one line below. C will be a constant mask indicating how many pixels the corresponding column moves: 0 or 1; it's just a convention. D, same as B (going down by 1 pixel).
The logical operation is (A & C) | (B & ~C). This should feel familiar to C2P users (half-merge?). But actually, it is just a multiplexer (or mux): https://en.m.wikipedia.org/wiki/Multiplexer#Digital_multiplexers
The interpretation is that pixels will come from A (one line above) if they need to move, or B if they don't.
In practice, the effect relies on tables containing the blit parameters for each block, for each frame within a quadrant. It is easier to generate those tables as a preprocessing step in a high-level language, than to do all those calculations at run time.
Now remains the question of how large the image can be. With a size of SxS, the blits cover about S x (S + 16) x 4 planes, using 2 sources. The "+ 16" comes from manipulating the image while it is sheared (remember that blocks are 16 pixels wide); it seems simpler to make all the blits of the same size. Mr. Pet uses an image of 160x160, but that seems small to me. I haven't programmed the Amiga since the 90's, so I don't remember well what to expect. My guess is that 224x224 is possible, while 256x256 would be a dream. Multiples of 32 are more handy in order to avoid a block spanning the centre, which would include some columns going down, but also some others going up (3 possible values). Reality check: in Turmoil, Mr. Pet mentions "spare processortime".
But he presumably had a bigger problem: the 1 pixel/frame "speed limit". The larger the image, the more this limit affects the rotation speed. With a 160x160, we need about 1000 angle steps to stay below the limit. 1024 is safe, with a full turn in 20.5s. Turmoil, with the same image size, seems to take about 26s. I don't know where the discrepency is coming from but it's also close enough, so I think I have covered the Turmoil version. By contrast, the Brian logo seems larger and turns in about 10s. That is the subject of layer 4 :)
Layer 4: faster rotation
------------------------
Warning: this section is more sketchy; to be honest, I initially expected to cover both versions in "just" 3 parts.
The Turmoil effect rotates very slowly, displaying artefacts more prominently. But we don't actually need to limit the absolute column speed to 1 pixel/frame; it is sufficient that columns within a block move at similar speeds, which is the case for shears. More precisely, we can restrict "movement distances" to only 2 values within a block: n and n+1, rather than 0 and 1 as in layer 3. Say we want to rotate 4x faster; due to the linear property of shears, the outer blocks will contain columns that move by either 3 or 4 pixels.
One change in the algorithm is that the blitter destination isn't always one of the sources anymore; the external program that generates the tables can provide this information. It seems that the blits should also be slightly increased in height: if you want to move a block n pixels down, you need to include n empty lines above the block, rather than just one. Reality check: this quote from earlier in this thread: "... describe what pixels, in that word, are to be plotted one line below all the other ones ..." seems to confirm that only movements of n or (n+1) are considered within a block.
So we can increase the rotation speed by a small factor, while also using a (presumably much) larger image. And I think we are done for the Brian version!
The end
-------
Credits:
- layers 1-3 by Mr. Pet
- layer 4 by Kreator/Anarchy?
Congratulations to them for an extremely intricate, while stunning (in the case of Brian anyway), effect!
Thanks for reading,
Xann.